Mathematics as a Complex Problem-Solving Activity
by Jacob Klerlein and Sheena Hervey, Generation Ready
By the time young children enter school they are already well along the pathway to becoming problem solvers. From birth, children are learning how to learn: they respond to their environment and the reactions of others. This making sense of experience is an ongoing, recursive process. We have known for a long time that reading is a complex problem-solving activity. More recently, teachers have come to understand that becoming mathematically literate is also a complex problem-solving activity that increases in power and flexibility when practiced more often. A problem in mathematics is any situation that must be resolved using mathematical tools but for which there is no immediately obvious strategy. If the way forward is obvious, it’s not a problem—it is a straightforward application.
Mathematicians have always understood that problem-solving is central to their discipline because without a problem there is no mathematics. Problem-solving has played a central role in the thinking of educational theorists ever since the publication of Pólya’s book “How to Solve It,” in 1945. The National Council of Teachers of Mathematics (NCTM) has been consistently advocating for problem-solving for nearly 40 years, while international trends in mathematics teaching have shown an increased focus on problem-solving and mathematical modeling beginning in the early 1990s. As educators internationally became increasingly aware that providing problem-solving experiences is critical if students are to be able to use and apply mathematical knowledge in meaningful ways (Wu and Zhang 2006) little changed at the school level in the United States.
“Problem-solving is not only a goal of learning mathematics, but also a major means of doing so.”
(NCTM, 2000, p. 52)
In 2011 the Common Core State Standards incorporated the NCTM Process Standards of problem-solving, reasoning and proof, communication, representation, and connections into the Standards for Mathematical Practice. For many teachers of mathematics this was the first time they had been expected to incorporate student collaboration and discourse with problem-solving. This practice requires teaching in profoundly different ways as schools moved from a teacher-directed to a more dialogic approach to teaching and learning. The challenge for teachers is to teach students not only to solve problems but also to learn about mathematics through problem-solving. While many students may develop procedural fluency, they often lack the deep conceptual understanding necessary to solve new problems or make connections between mathematical ideas.
“A problem-solving curriculum, however, requires a different role from the teacher. Rather than directing a lesson, the teacher needs to provide time for students to grapple with problems, search for strategies and solutions on their own, and learn to evaluate their own results. Although the teacher needs to be very much present, the primary focus in the class needs to be on the students’ thinking processes.”
(Burns, 2000, p. 29)
Learning to problem solve
To understand how students become problem solvers we need to look at the theories that underpin learning in mathematics. These include recognition of the developmental aspects of learning and the essential fact that students actively engage in learning mathematics through “doing, talking, reflecting, discussing, observing, investigating, listening, and reasoning” (Copley, 2000, p. 29). The concept of co-construction of learning is the basis for the theory. Moreover, we know that each student is on their unique path of development.
Beliefs underpinning effective teaching of mathematics
- Every student’s identity, language, and culture need to be respected and valued.
- Every student has the right to access effective mathematics education.
- Every student can become a successful learner of mathematics.
Children arrive at school with intuitive mathematical understandings. A teacher needs to connect with and build on those understandings through experiences that allow students to explore mathematics and to communicate their ideas in a meaningful dialogue with the teacher and their peers.
Learning takes place within social settings (Vygotsky, 1978). Students construct understandings through engagement with problems and interaction with others in these activities. Through these social interactions, students feel that they can take risks, try new strategies, and give and receive feedback. They learn cooperatively as they share a range of points of view or discuss ways of solving a problem. It is through talking about problems and discussing their ideas that children construct knowledge and acquire the language to make sense of experiences.
Students acquire their understanding of mathematics and develop problem-solving skills as a result of solving problems, rather than being taught something directly (Hiebert1997). The teacher’s role is to construct problems and present situations that provide a forum in which problem-solving can occur.
Why is problem-solving important?
Our students live in an information and technology-based society where they need to be able to think critically about complex issues, and “analyze and think logically about new situations, devise unspecified solution procedures, and communicate their solution clearly and convincingly to others” (Baroody, 1998). Mathematics education is important not only because of the “gatekeeping role that mathematics plays in students’ access to educational and economic opportunities,” but also because the problem-solving processes and the acquisition of problem-solving strategies equips students for life beyond school (Cobb, & Hodge, 2002).
The importance of problem-solving in learning mathematics comes from the belief that mathematics is primarily about reasoning, not memorization. Problem-solving allows students to develop understanding and explain the processes used to arrive at solutions, rather than remembering and applying a set of procedures. It is through problem-solving that students develop a deeper understanding of mathematical concepts, become more engaged, and appreciate the relevance and usefulness of mathematics (Wu and Zhang 2006). Problem-solving in mathematics supports the development of:
- The ability to think creatively, critically, and logically
- The ability to structure and organize
- The ability to process information
- Enjoyment of an intellectual challenge
- The skills to solve problems that help them to investigate and understand the world
Problem-solving should underlie all aspects of mathematics teaching in order to give students the experience of the power of mathematics in the world around them. This method allows students to see problem-solving as a vehicle to construct, evaluate, and refine their theories about mathematics and the theories of others.
Problems that are “Problematic”
The teacher’s expectations of the students are essential. Students only learn to handle complex problems by being exposed to them. Students need to have opportunities to work on complex tasks rather than a series of simple tasks devolved from a complex task. This is important for stimulating the students’ mathematical reasoning and building durable mathematical knowledge (Anthony and Walshaw, 2007). The challenge for teachers is ensuring the problems they set are designed to support mathematics learning and are appropriate and challenging for all students. The problems need to be difficult enough to provide a challenge but not so difficult that students can’t succeed. Teachers who get this right create resilient problem solvers who know that with perseverance they can succeed. Problems need to be within the students’ “Zone of Proximal Development” (Vygotsky 1968). These types of complex problems will provide opportunities for discussion and learning.
Students will have opportunities to explain their ideas, respond to the ideas of others, and challenge their thinking. Those students who think math is all about the “correct” answer will need support and encouragement to take risks. Tolerance of difficulty is essential in a problem-solving disposition because being “stuck” is an inevitable stage in resolving just about any problem. Getting unstuck typically takes time and involves trying a variety of approaches. Students need to learn this experientially. Effective problems:
- Are accessible and extendable
- Allow individuals to make decisions
- Promote discussion and communication
- Encourage originality and invention
- Encourage “what if?” and “what if not?” questions
- Contain an element of surprise (Adapted from Ahmed, 1987)
“Students learn to problem solve in mathematics primarily through ‘doing, talking, reflecting, discussing, observing, investigating, listening, and reasoning.”
(Copley, 2000, p. 29)
“…as learners investigate together. It becomes a mini- society – a community of learners engaged in mathematical activity, discourse and reflection. Learners must be given the opportunity to act as mathematicians by allowing, supporting and challenging their ‘mathematizing’ of particular situations. The community provides an environment in which individual mathematical ideas can be expressed and tested against others’ ideas.…This enables learners to become clearer and more confident about what they know and understand.”
(Fosnot, 2005, p. 10)
Research shows that‘classrooms where the orientation consistently defines task outcomes in terms of the answers rather than the thinking processes entailed in reaching the answers negatively affects the thinking processes and mathematical identities of learners’ (Anthony and Walshaw, 2007, page 122).
Effective teachers model good problem-solving habits for their students. Their questions are designed to help children use a variety of strategies and materials to solve problems. Students often want to begin without a plan in mind. Through appropriate questions, the teacher gives students some structure for beginning the problem without telling them exactly what to do. In 1945 Pólya published the following four principles of problem-solving to support teachers with helping their students.
- Understand and explore the problem
- Find a strategy
- Use the strategy to solve the problem
- Look back and reflect on the solution
Problem-solving is not linear but rather a complex, interactive process. Students move backward and forward between and across Pólya’s phases. The Common Core State Standards describe the process as follows:
“Mathematically proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. They analyze givens, constraints, relationships, and goals. They make conjectures about the form and meaning of the solution and plan a solution pathway rather than simply jumping into a solution attempt. They consider analogous problems, and try special cases and simpler forms of the original problem in order to gain insight into its solution. They monitor and evaluate their progress and change course if necessary”. (New York State Next Generation Mathematics Learning Standards 2017).
Pólya’s Principals of Problem-Solving
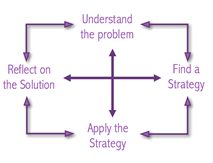
- Understand and explore the problem
- Find a strategy
- Use the strategy to solve the problem
- Look back and reflect on the solution
Students move forward and backward as they move through the problem-solving process.
The goal is for students to have a range of strategies they use to solve problems and understand that there may be more than one solution. It is important to realize that the process is just as important, if not more important, than arriving at a solution, for it is in the solution process that students uncover the mathematics. Arriving at an answer isn’t the end of the process. Reflecting on the strategies used to solve the problem provides additional learning experiences. Studying the approach used for one problem helps students become more comfortable with using that strategy in a variety of other situations.
When making sense of ideas, students need opportunities to work both independently and collaboratively. There will be times when students need to be able to work independently and other times when they will need to be able to work in small groups so that they can share ideas and learn with and from others.
Getting real
Effective teachers of mathematics create purposeful learning experiences for students through solving problems in relevant and meaningful contexts. While word problems are a way of putting mathematics into contexts, it doesn’t automatically make them real. The challenge for teachers is to provide students with problems that draw on their experience of reality, rather than asking them to suspend it. Realistic does not mean that problems necessarily involve real contexts, but rather they make students think in “real” ways.
Planning for talk
By planning for and promoting discourse, teachers can actively engage students in mathematical thinking. In discourse-rich mathematics classes, students explain and discuss the strategies and processes they use in solving mathematical problems, thereby connecting their everyday language with the specialized vocabulary of mathematics.
Students need to understand how to communicate mathematically, give sound mathematical explanations, and justify their solutions. Effective teachers encourage their students to communicate their ideas orally, in writing, and by using a variety of representations. Through listening to students, teachers can better understand what their students know and misconceptions they may have. It is the misconceptions that provide a window into the students’ learning process. Effective teachers view thinking as “the process of understanding,” they can use their students’ thinking as a resource for further learning. Such teachers are responsive both to their students and to the discipline of mathematics.
“Mathematics today requires not only computational skills but also the ability to think and reason mathematically in order to solve the new problems and learn the new ideas that students will face in the future. Learning is enhanced in classrooms where students are required to evaluate their own ideas and those of others, are encouraged to make mathematical conjectures and test them, and are helped to develop their reasoning skills.”
(John Van De Walle)
“Equity. Excellence in mathematics education requires equity—high expectations and strong support for all students.”
(NTCM)
Conclusion
How teachers organize classroom instruction is very much dependent on what they know and believe about mathematics and on what they understand about mathematics teaching and learning. Teachers need to recognize that problem-solving processes develop over time and are significantly improved by effective teaching practices. The teacher’s role begins with selecting rich problem-solving tasks that focus on the mathematics the teacher wants their students to explore. A problem-solving approach is not only a way for developing students’ thinking, but it also provides a context for learning mathematical concepts. Problem-solving allows students to transfer what they have already learned to unfamiliar situations. A problem-solving approach provides a way for students to actively construct their ideas about mathematics and to take responsibility for their learning. The challenge for mathematics teachers is to develop the students’ mathematical thinking process alongside the knowledge and to create opportunities to present even routine mathematics tasks in problem-solving contexts.
Given the efforts to date to include problem-solving as an integral component of the mathematics curriculum and the limited implementation in classrooms, it will take more than rhetoric to achieve this goal. While providing valuable professional learning, resources, and more time are essential steps, it is possible that problem-solving in mathematics will only become valued when high-stakes assessment reflects the importance of students’ solving of complex problems.
